Arbitrage betting
Betting arbitrage, miraclebets, surebets, sports arbitraging is a particular case of arbitrage arising on betting markets due to either bookmakers’ different opinions on event outcomes or plain errors. By placing one bet per each outcome with different betting companies, the bettor can make a profit. As long as different Bookmakers are used for arbitrage betting the Bookmakers do not have a problem with this. Each Bookmaker will still make profit due to their calculations.
In the bettors’ slang an arbitrage is often referred to as an arb; people who use arbitrage are called arbers. A typical arb is around 2%, often less, however 4%-5% are also normal and during some special events they might reach 20%.
Arbitrage Betting involves relatively large sums of money (stakes are bigger than in normal betting) while another variety, betting investment, means placing relatively small bets systematically on overvalued odds most of which will lose but some win thus making a profit.
The best way of generating profit, which has been established in Britain via sports arbitrage, consists of ‘key men’ employing others to place bets on their behalf, so as to avoid detection and increase accessibility to bookmakers. This allows the financiers or key arbers to stay at a computer to keep track of market movement.
Arbitrage in theory
There are a number of potential arbitrage deals. Below is an explanation of some of them including formulas and risks associated with these arbitrage deals. The table below introduces a number of variables that will be used to formalise the arbitrage models.
| Variable | Explanation |
| s1 | Stake in outcome 1 |
| s2 | Stake in outcome 2 |
| o1 | Odds for outcome 1 |
| o2 | Odds for outcome 2 |
| r1 | Return if outcome 1 occurs |
| r2 | Return if outcome 2 occurs |
Arbitrage using bookmakers
This type of arbitrage takes advantage of different odds offered by different bookmakers. Assume the following situation:
We consider an event with 2 possible outcomes (e.g. a tennis match – either Federer wins or Henman wins), the idea can be generalized to events with more outcomes, but we use this as an example.
The 2 bookmakers have different ideas of who has the best chances of winning. They offer the following Fixed-odds gambling on the outcomes of the event
| Bookmaker 1 | Bookmaker2 | |
| Outcome 1 | 1.25 | 1.43 |
| Outcome 2 | 3.9 | 2.85 |
For an individual bookmaker, the sum of the inverse of all outcomes of an event will always be greater than 1. 1.25 − 1 + 3.9 − 1 = 1.056 and 1.43 − 1 + 2.85 − 1 = 1.051
The fraction above 1, is the bookmakers return rate, the amount the bookmaker earns on offering bets at some event. Bookmaker 1 will in this example expect to earn 5.6% on bets on the tennis game. Usually these gaps will be in the order 8 – 12%.
The idea is to find odds at different bookmakers, where the sum of the inverse of all the outcomes are below 1. Meaning that the bookmakers disagree on the chances of the outcomes. This discrepancy can be used to obtain a profit.
For instance if one places a bet on outcome 1 at bookmaker 2 and outcome 2 at bookmaker 1:
1.43 − 1 + 3.9 − 1 = 0.956
Placing a bet of 100$ on outcome 1 with bookmaker 2 and a bet of $100 * 1.43 / 3.9 = 36.67 on outcome 2 at bookmaker 1 would ensure the bettor a profit.
In case outcome 1 comes out, one could collect r1 = $100 * 1.43 = $143 from bookmaker 2. In case outcome 2 comes out, one could collect r2 = $36.67 * 3.9 = $143 from bookmaker 1. One would have invested $136.67, but have collected $143, a profit of $6.33 (%4.6) no matter the outcome of the event.
So for 2 odds o1 and o2, where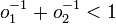 
. If one wishes to place stake s1 at outcome 1, then one should place s2 = s1 * o1 / o2 at outcome 2, to even out the odds, and receive the same return no matter the outcome of the event.
Or in other words, if there are two outcomes, a 2/1 and a 3/1, by covering the 2/1 with $500 and the 3/1 with $333, one is guaranteed to win $1000 at a cost of $833, giving a 20% profit. More often profits exists around the 4% mark or less.
Reducing the risk of human error is vital being that the mathematical formula is sound and only external factors add “risk”. Numerous online arbitrage calculator tools exist to help bettors get the math right. For example, arb calculators can handle calculations for both book arbitrage (back/back or lay/lay) and back/lay arbitrage opportunities on an intra-exchange or inter-exchange basis, and is free.
Back-lay sports arbitrage
Betting exchanges have opened up a new range of arbitrage possibilities since on the exchanges it is possible to lay (i.e. to bet against) as well as to back an outcome. Arbitrage using only the back or lay side might occur on betting exchanges. It is in principle the same as the arbitrage using different bookmakers. Arbitrage using back and lay side is possible if a lay bet on one exchange provides shorter odds than a back bet on another exchange or bookmaker. However, the commission charged by the bookmakers and exchanges must be included into calculations.
Back-lay sports arbitrage is often called scalping or trading. Scalping is not actually arbitrage, but short term trading. In the context of sports arbitrage betting a scalping trader or scalper looks to make lots of small profits, which in time can add up. In theory a trader could turn a small investment into large profits by re-investing his earlier profits into future bets so as to generate exponential growth. Scalping relies on liquidity in the markets and that the odds fill fluctuate around a mean point. A key advantage to scalping on one exchange is that most exchanges charge commission only on the net winnings in a particular event, thus ensuring that even the smallest favorable difference in the odds will guarantee some profit.
Bonus sports arbitrage
Many bookmakers offer first time users a signup bonus in the range $10 – $200 for depositing an initial amount. They typically demand that this amount is wagered a number of times before the bonus can be withdrawn. Bonus sport arbitraging is a form of sports arbitraging where you hedge or back your bets as usual, but since you received the bonus, a small loss can be allowed on each wager (2-5 %), which comes off your profit. In this way the bookmakers wagering demand can be met and the initial deposit and sign up bonus can be withdrawn with little loss.
The advantage over usual betting arbitrage is that it is a lot easier to find bets with an acceptable loss, instead of an actual profit. Since most bookmakers offer these bonuses this can potentially be exploited to harvest the sign up bonuses.
Making money:
By signing up to various bookmakers, it’s possible to turn these ‘free’ bets into cash fairly quickly, and either making a small arbitrage, or in the majority of cases, making a small loss on each bet, or trade. However, it is relatively time consuming to find close matched bets or arbs, which is where an arb / close matched bet service is useful.
Drawbacks:
As well as spending time physically matching odds from various bet sites to exchanges, the other draw back with bonus bagging / arb trading in this sense is that often the free bets are ‘non-stake returned’. This effectively reduces the odds, in decimal format, by 1. Therefore, in order to reduce ‘losses’ on the free bet, it is necessary to place a bet with high odds, so that the percentage difference of the decrease in odds is minimised.
Arbitrage in practice
While often claimed to be “risk-free”, this is only true if an arb is successfully completed; in reality, there are several threats to this:
Disappearance of arb: Arbs in online sports markets have a median lifetime of around 15 minutes, after which the difference in odds undepinning them vanishes through betting activity. Without rapid alerting and action, it is possible to fail to make all the “legs” of the arb before it vanishes, thus transforming it from a risk-free arb into a bet. High street bookmakers however, offer their odds days in advance and rarely change them once they’ve been set. These arbs can have a lifetime of several hours.
Making errors: In the excitement of the action and due to the high number of bets placed, it is not uncommon to make a mistake (like traders on financial markets). For example the appropriate stakes may be incorrectly calculated, or be placed on the wrong “legs” of the arb, locking in a loss, or there may be inadequate funds in one of the accounts to complete the arb. Those errors might temporarily have an important impact. In the long term, the benefit will depend on the odds. For example one could actually make more money by placing the “wrong” bet where the outcome happens to be beneficial, though not justified by the arbitrage calculation. However, this stroke of luck being repeated is unlikely, assuming the bookies have calculated the odds so they make a profit.
Bet cancellation: If a bettor places bets so as to make an arbitrage and one bookmaker cancels a bet, the bettor could find himself in a bad position because he is actually betting with all the risks implied. The bettor can repeat the bet that has been cancelled so as minimize the risk, but if he cannot get the same odds he had before he may be forced to take a loss. In some cases the situation arises when there are very high potential payouts by the bookie, perhaps due to an unintentional error made while quoting odds. Many jurisdictions allow bookmakers to cancel bets in the event of such a “palpable” [“obvious”] error in the quoted odds This is often loosely defined as an obvious mistake, but whether a “palp” in fact has been made is often the sole discretion of the bookmaker.
Other Problems: Bookmakers who suspect arbing can set very low maximum stake limits, making arbing insufficiently profitable. Capital diffusion is serious; many bookmakers make it very easy to deposit funds and difficult to withdraw them. Making a return involves many bets spread over typically many bookmakers so keeping track is a considerable challenge, and requires excellent record-keeping.